介绍
timsort结合了插入排序和合并排序,主要是考虑到了,把每段有规律的数据分块,块的长度一开始计算好。然后有的数据块长度不足时使用插入补充。最后合并所有数据块。
所以整个算法就是数据越规律,性能越高,整体性能甚至超过了快排: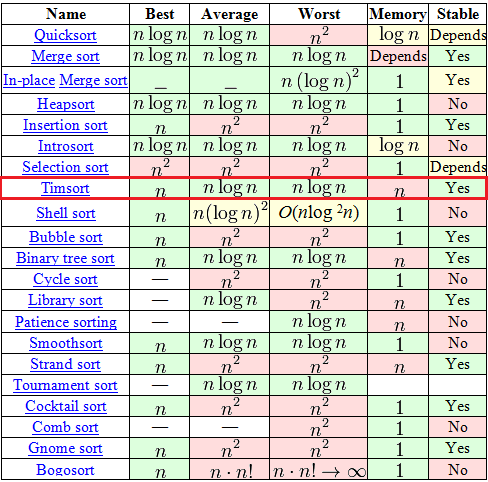
过程
定义
- minrun 块长度
- N 数组长度
确定minrun
minrun根据输入数组的长度计算,因为块的长度影响最后合并的次数,如果块长度太短那么合并次数过多;太长那么要把每个块长度凑齐,插入排序的操作又太多。力求最后合并的次数是2的幂或略小于。1
2
3
4
5
6
7
8
9int GetMinrun(int n)
{
int r = 0;
while (n >= 64) {
r |= n & 1;
n >>= 1;
}
return n + r;
}
上面的公式说明:当N<64的时候,minrun=N;当N>=64;minrun与N最低6位有关
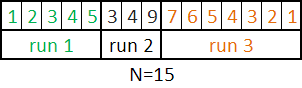
分块
开始扫描,把有序的元素存入当前的run(块),如果这时候run长度小于minrun,那么直接添加后面缺的元素,知道长度达到minrun,这个时候后面的元素就不一定有序的,那么这个块需要进行插入排序。
当然如果数据一直有序,那么run的长度就会比minrun大
ex:
1 2 3 4 2 ….
N = b10000 011111, minrun=5。run=[1, 2, 3, 4],还是有序的。但是再加上2就不是有序,这个时候需要插入排序,变成[1, 2, 2, 3, 4]
合并
依次把run压进栈,然后判断下面的两个条件是否满足:
- X > Y + Z
- Y > Z
如果有一个不满足,那么找出X和Z中比较小的一个,和Y合并。直到满足了条件或者所有数据都排好序。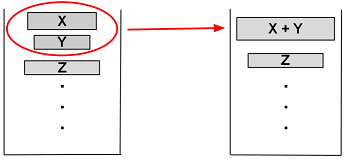
(X、Y、Z表示run的size)
(想象一个理想的例子:有一个128、64、32、16、8、4、2和2的运行(让我们暂时忘记运行大小≥minrun的要求)。在这种情况下,在最后两次运行不满足之前不会有任何合并,然后将执行七个完全平衡的合并。)
测试
1 | #coding:utf-8 |
结果:
[0.07372325937786056, 0.07182481873564303, 0.07235884537346904]
[0.7830219300524532, 0.7451907132607314, 0.735450580565536]
[7.420490329467173, 7.352885764485594, 7.402370308503823]
(这说明只要先排序了排行榜,那么1s的刷新可以达到10w次)


评论加载中